今天看到一个有趣的问题,
想象着,有一个房间,里面有 100 个人,每个人有 100 美元。每过一会,每个有钱的人给随机的其他人 1 美元,经过一段时间后,房间内的资金分配情况是怎样?
粗想想,每个人都是“相同的概率”丢失和获得一元钱,那么大家的资金应该大差不差才是,可惜后面的结果大打脸,贫富差距居然那么明显,实在是非常的反直觉,于是我用JS写了个模拟程序跑跑看。
地址在 https://jsfiddle.net/chxw4kLs/ ,使用Vue来显示图形化的效果,红色的柱状图是0~99号的资金情况,半透明的蓝色是排序后的结果,方便查看。下面文字是最富,最穷,以及首富的变动情况。
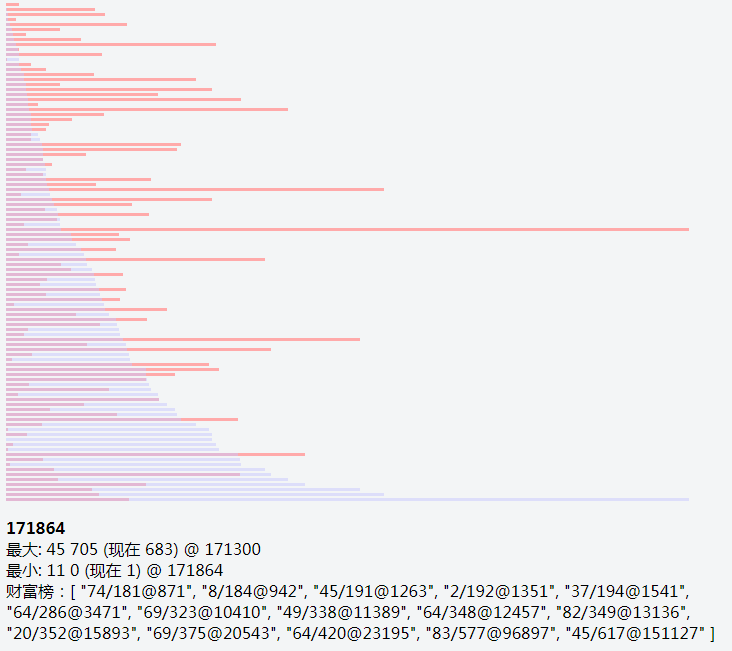
结果真的非常出人意料,跑了一段时间后,最富的人已然拥有700多美元,而贫穷的人早已是0元家当。
代码用了一些ES6的东西,可能要比较新的浏览器才能查看效果,Vue真的很好使,这样的一个界面虽然不复杂,但是写的还是挺舒服的。
为什么有人富有人穷呢,即便实在这样一种“公平”的环境下,还是产生了如此悬殊的贫富差距,这就是命运吗?而我们的社会其实并没有那么公平,所以…… 我陷入了深深的沉思?
很有意思,好像有点正态分布的意思
恐怕真的和随机分布有什么关系
我也试了一下,感觉应该是正态分布
仔细想了一下,任意一人的资金变化应该是符合有边界(0~10,000)的random walk概率模型。
知乎上的问题吧?最近也看到过
蛮有意思的
我觉得直觉没错啊 不管怎么说大家概率一样的话数量够大就会差不多的啊
环境渐渐达到稳态,我偏向用化学的角度去解释,绝对的公平是不稳定的,所以才会有贫富差距
那其实每个人成为那个最富有与最贫穷的人的概率是一样的啊。
很简单,
如果“钱”在给了别人以后自己的总量没有减少,
那么总量会不断增长
假设演化简单地服从 x’ = 2 * x
即x变成原来的2倍,用图像表示就是:
——-
——–
———-
演化变成:
————–
—————-
——————–
演化变成:
—————————-
——————————–
—————————————-
演化变成:
——————————————————–
—————————————————————-
——————————————————————————–
可以发现数目不断增长,导致差距越来越大,比例没有变化
但是如果每一个x在分配以后都要-1,相当于在增加以后砍掉一截
——-
——–
———-
演化变成:
——|——–
——|———-
——|————–
演化变成:
——————|———-
——————-|————-
——————|———————-
演化变成:
—————————————–|—————
——————————————|———————-
——————————————|————————————–
这样`|`右边的部分就有了明显的差距,
原因在于比例不变,但是因为不-1的总量增大,`|`右边的差距会增大
根本原因在于钱是物质,从A手里到B手里,A的钱会减少。而不是像信息一样具有可复制性。
没看懂这是怎么算的?
以太效应太残酷,ES6有好多新东西啊
是马太效应
js的随机函数并不是真随机,请用完全的真随机算法试试
首先第一次分配钱的时候,必然产生一个101和一个99,此时极差为2。第二次分配的时候,又会产生一组极差,如果要尽量减少总极差,那么此时应该正好抹消第一次的那一组,即第一次的两个人把身份对调,这样两个人又回到了100.然而这种概率极小,因此可以近似地看成每一次分配钱的时候,都在增加系统的差距。即便如此,如果系统的差距能在多次之后得到修复也还是可以扭转的,然而这是不可能的,既然每一次分配都是相同的原则,那么证明了两次分配,就可以证明20次,200次,2000次分配都没有本质差别,系统的总差距必然不断增加。
…